このブログで使用しているVer
・Unity 2021.3.0f1

こんにちは!個人でゲームをコツコツ作っています。えきふるです!
自分のゲームにガチャっぽい機能をつけたい!でも調べたけどよくわからん!そんなこと誰にでもありますよね。私もです。
そんな私でも(一週間くらい調べたり検証したりしたけど)多分理解できたので、ここでは重み付きの確率計算について記載いたします!
この記事はこんな人向け!
- 確率計算ってUnityでどうやるの?
- 初心者にもわかるように長くても良いから詳しく教えてよ〜。
- レア判定のあるガチャのアルゴリズムを知りたい。
- 重み付き抽選ってなんなん?
先にサンプルコードを掲載します。
このサンプルの中身、説明が興味がある方は順に見ていきましょう!
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class gatya : MonoBehaviour
{
float[] item;
//ガチャを引くメソッド
public void Gatya()
{
//アイテムの配列に重みを設定していく。
item = new float[5];
item[0] = 5;
item[1] = 20;
item[2] = 20;
item[3] = 100;
item[4] = 100;
//抽選メソッドを呼ぶ
var result = Choose(item);
Debug.Log(result);
}
//ローカル関数
float Choose(float[] probs)
{
float total = 0;
//配列の要素を代入して重みの計算
foreach (float elem in probs)
{
total += elem;
}
//重みの総数に0から1.0の乱数をかけて抽選を行う
float randomPoint = Random.value * total;
//iが配列の最大要素数になるまで繰り返す
for (int i = 0; i < probs.Length; i++)
{
//ランダムポイントが重みより小さいなら
if (randomPoint < probs[i])
{
return i;
}
else
{
//ランダムポイントが重みより大きいならその値を引いて次の要素へ
randomPoint -= probs[i];
}
}
//乱数が1の時、配列数の-1=要素の最後の値をChoose配列に戻している
return probs.Length - 1;
}
}
まずはプログラムの説明より先に、抽選のアルゴリズムの説明からしますふる!
重み付きのガチャ抽選/確率計算とは
重み付きの確率計算とはくじ引きや商店街の景品でよくあるガラガラのような抽選方法の確率の事を言います。
ガラガラやくじ引きでは
1等・・・世界旅行(1名)
2等・・・MacBook(5名)
・
・
ハズレ・・・ティッシュ
のように景品にはレア度(等級)によってその数(当選数)が定められており、当たりやすさが違いますよね。
このような同じ場所から選ぶ時に種類によって当たる確率が違う選択方法を重み付き抽選、と言います。
ゲームで言えばレア付きのガチャや、敵の落とすアイテムにレアドロップがあるものや、ローグライクゲームの出現アイテムの確率判定なんかにも使えそうです。
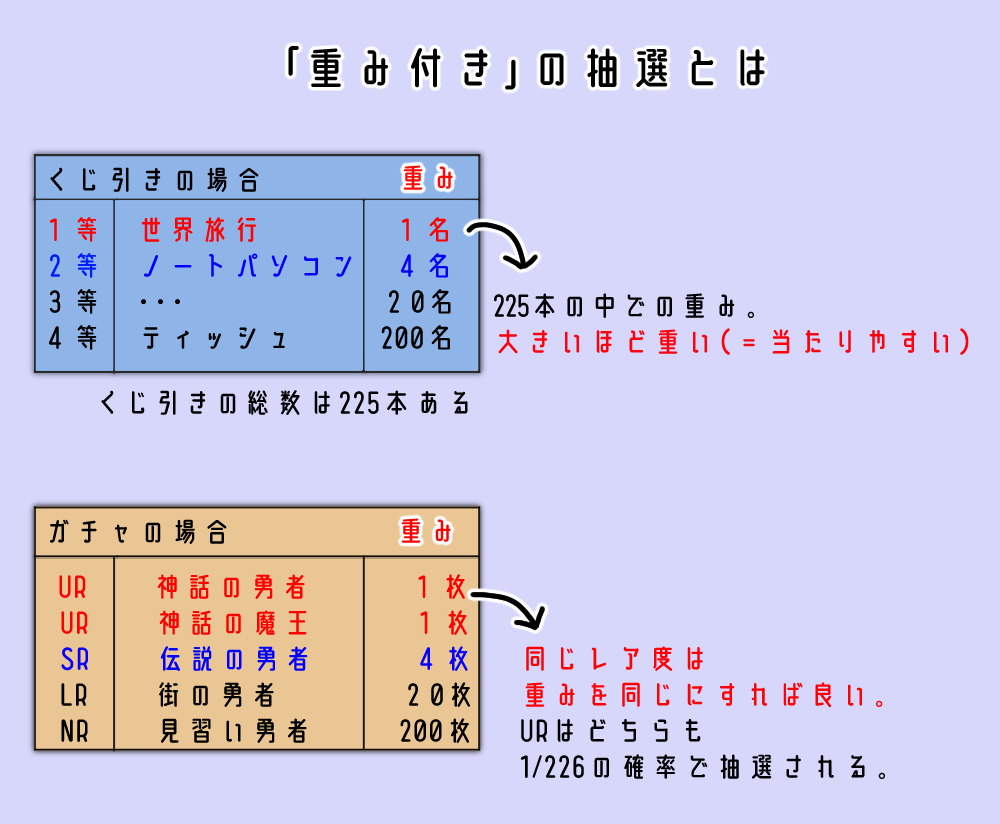
重みはratio(=比率)という言われ方もして、
全体に対しての数字が大きければ大きいほど当選がしやすくなっている状態ですね。

もしクジ引きで一等が「1万本」あったらめっちゃ当たるふるね!?

…でもクジの総数が100兆本あったらそんな事ないふるよね?
つまり重みの当たり易さは全体の数に依存するふるね〜
TIPS:なんで重み付きって言うの?
直線上に1個、2個、3個、、、n個と重みがバラバラのものを置いた時、この平均の位置(重心)を求めるために全体の重みから個別の重みを考慮して計算していくこと(=加重平均というらしい)が由来見たい。

つまり数学的な用語らしい
重み付きガチャの抽選判定
重み付き抽選の判定、つまり抽選したものが何だったか?の判定は
帯状のバーにダーツを投げてどこに刺さったかを求めるようなイメージと同じです。
ダーツ(=乱数)が当たった場所を★とした時に★は帯のどこにあるのか?
をそれぞれの色のエリア内で確認処理させていけば出すことができます。


どういう事か細かく見ていきましょう!
抽選結果の割り出し方

順を追って解説を頑張ってみますふるので、もう少し付き合って下さいふる。
まず、1回サイコロを振った時に1の目が出る確率は?と言われたら6分の1ですね。
この6分の1の確率は1÷6≒16.7%です。
1の目の数/全ての目の数となります。
では下記の場合はどうでしょうか。
箱の中に15個のクジがあり、それぞれ
金のクジが1個
銀のクジが4個
白のクジが10個
あります。
この時、それぞれの色のクジが出る確率はサイコロの時と同様の考え方で
特定の色の個数/全ての個数となるので
金のクジ・・・15分の1=1/15 ≒6.6%
銀のクジ・・・15分の4=4/15 ≒26.7%
白のクジ・・・15分の10=10/15 ≒66.7%
となり、これら全てを合計すると100%になります。
これは重みの総数15を100%に置き換えた時のそれぞれの確率がという事ですね。
ここまで確率の出し方を考えてきましたが、
私達は個別の当選確率を出したいのではなく、引いたクジがどれに当選したのか?を知りたいんですよね。

何%で当たるか?を知りたいわけじゃないふる!
どこに当選したか、は下記のように考えられます。
・クジ引きの金を1番、銀を2番〜5番、白を6番〜15番と数字を振り、ランダムに決めた数字が金、銀、白のどのエリアの数字か?
これはこの項の冒頭で言った
・ダーツで1等2等3等・・・と的に書いてランダムに投げた時にどのエリアに刺さったか?
と同じ事です。
そしてこれを少し抽象的にすると
・帯状のバーをそれぞれの重みに比例して並べて、ランダムに選んだ数字がどのエリアにあるか?
となります。

そしてこの時、全体の総数15を100%とすると
0〜100%の中で1等2等3等は先ほどの確率の出し方(特定の値/全ての値)
のパーセント分で埋まることになります。
その中で乱数で得られた0〜100までの数はどの等級の場所にいたか?となります。

乱数で得られた値(図の赤い星)をaとすると、
このaがどの等級エリアにいるかが分かれば判定ができるということになりますよね。
aがどこにいるのかを判定するには、図の例の場合
・0%〜7%の間か?
・7%〜33%の間か?
・33%〜100%の間か?
これを順に確認して成立するものを探せば見つかります。
これを不等式にすると、aの位置の割り出し方は
・0 ≦a<7
・7 ≦a< 33
・33≦a< 100
この成否を確認していく事になります。

これが重み付きガチャの基本的な判定構造になります。

理論は分かったので、実際にプログラムではどのように書いていくか見ていきましょう!
TIPS:重み付け抽選の利点
重み付けの利点は、重みの総数を100%に変換しているので
全体の個数を100の値に調整する必要が無く、それぞれを比べた時の当たりやすさだけ注意をすればいい事です。
これにより、後からアイテムを追加したり、介入したりすることも安易です。
全体との比率なので常に固定の確率にすることは逆に面倒ですが、
ステージ毎に出現するアイテムを変えたりすることが出来るので、ローグライクゲーム等で有効です。
Unity C#プログラムでガチャのアルゴリズムを作成

やっとここまで来たふる!
それでは実際のコードを見ていきましょう。
下記のコードでは
Gatya関数を呼び出すとアイテム用の配列を生成し抽選を行い、
選ばれたアイテム=配列要素を返す、という流れになっています。
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class gatya : MonoBehaviour
{
float[] item;
//ガチャを引くメソッド
public void Gatya()
{
//アイテムの配列に重みを設定していく。
item = new float[5];
item[0] = 5;
item[1] = 20;
item[2] = 20;
item[3] = 100;
item[4] = 100;
//抽選メソッドを行い、resultに配列の要素の数字を返す。
var result = Choose(item);
Debug.Log(result);
}
//ローカル関数
float Choose(float[] probs)
{
float total = 0;
//配列の要素を代入して重みの計算
foreach (float elem in probs)
{
total += elem;
}
//重みの総数に0から1.0の乱数をかけて抽選を行う
float randomPoint = Random.value * total;
//iが配列の最大要素数になるまで繰り返す
for (int i = 0; i < probs.Length; i++)
{
//ランダムポイントが重みより小さいなら
if (randomPoint < probs[i])
{
return i;
}
else
{
//ランダムポイントが重みより大きいならその値を引いて次の要素へ
randomPoint -= probs[i];
}
}
//乱数が1の時、配列数の-1=要素の最後の値をChoose配列に戻している
return probs.Length - 1;
}
}それでは上から順に詳しく見ていきましょう!

長いけどその分丁寧に出来るようにがんばります!
float[] item;まず抽選を行うアイテムを入れる為の配列変数を作成します。
public void Gatya()
{
//アイテムの配列に重みを設定していく。
item = new float[5];
item[0] = 5;
item[1] = 20;
item[2] = 20;
item[3] = 100;
item[4] = 100;
//抽選メソッドを行い、resultに配列の要素の数字を返す。
var result = Choose(item);
Debug.Log(result);
}ここのGatyaメソッドで
アイテム用の配列をfloat型でインスタンス作成します。今回は5つ作成しました。
配列についてわからない方はこちらで説明していますのでご確認下さいませ!
作成した配列の要素にそれぞれ数字を代入していきます。
この数字が重みになります。
var result = Choose(item);
Debug.Log(result);その後、ここでitem配列を引数として入れてChoose関数を呼び出し、
その結果をresultとして得ます。

Choose関数の中でどんな処理をしているか見てみよう
float Choose(float[] probs)引数を入れて呼び出されるfloat型のローカル関数Chooseです。
ローカル関数とは関数の中に記述する関数のことですが、
C#の場合はメソッドと殆ど同じように扱えます。
記述のルールは下記。※上の記述では修飾子は省いてます。
修飾子 戻り値の型 メソッド名(引数リスト)
float total = 0;
//配列の要素を代入して重みの計算
foreach (float elem in probs)
{
total += elem;
}
まずfloat型のtotalに0を代入します。初期化しているだけです。
foreach文でfloat型の変数elemに配列probsの要素を順に代入して処理します。
処理内容はtotalに配列の要素の中身を順に全て足していきます。
これが重みの総量=100%の値になります。
ここでのprobsは先ほど引数で代入しているので配列変数itemになっています。
※foreach文はあるデータ集合体に対して処理を一通り実行するループ文。
float randomPoint = Random.value * total;次に重みの総量にRandom.valueで0〜1.0の乱数をかけます。ここで抽選を行っています。
これは重みの総量の中からランダムの数字を引いている事と同じです。
//iが配列の最大要素数になるまで繰り返す
for (int i = 0; i < probs.Length; i++)
{
//ランダムポイントが重みより小さいなら
if (randomPoint < probs[i])
{
return i;
}
else
{
//ランダムポイントが重みより大きいならその値を引いて次の要素へ
randomPoint -= probs[i];
}
}ここではforループ文の中で抽選結果がどの配列の要素の値を選んだかを判定、
returnで戻り値としてGatya()メソッドのresultに返しています。
つまりダーツの位置を調べる処理を行なっています。
forループの中では変数iをprobs.Length=配列の要素の最大数になるまで、
if分の処理をする度に+1させてループ処理しています。
if文の中では
randomPoint(=抽選結果の値)が配列の要素probs[i](=重み)より小さければiを抽選の結果としてresultに返しています。
iより小さくなかった場合は抽選結果の数から配列の要素iの重みを引いた値を抽選結果の数に入れ直して再度判定処理を行います。
これはどういう事でしょうか。
一度数式で考えてみます。
抽選結果の値randomPointがどこの値に該当するかを調べるには、
配列の重みの値を順に並べて、不等式が成立するかで判定していく必要があります。今回の場合、
item[0] = 5;
item[1] = 20;
item[2] = 20;
item[3] = 100;
item[4] = 100;なので、これを不等式にすると
item[0] 0 ≦ randomPoint < 5
item[1] 5 ≦ randomPoint < 25
item[2] 25 ≦ randomPoint < 45
item[3] 45 ≦ randomPoint < 145
item[4] 145 ≦ randomPoint < 245
となり、この不等式が成立するrandomPointを探す事になります。
この時、0 ≦ randomPoint < 5じゃなかったら5 ≦ randomPoint < 25を判定して・・・・と
コードに順に書くこともできると思いますが、
そうすると重み付きの新しいアイテムを追加する度にコードを打ち直さなければいけません。
そこで、この不等式をよく見ると
2回目以降の判定している「数字≦」の数字部分は
前の判定の「<数字」の値と同じになっていますよね。
また、randomPointが0以上なのは重みの総数(正)に0〜1.0の乱数(正)をかけているので明らかです。
そこで全ての不等式を0≦に揃えて見ると
item[0] 0 ≦ randomPoint < 5
item[1] 0 ≦ randomPoint-5 < 20
item[2] 0 ≦ randomPoint-20 < 20
item[3] 0 ≦ randomPoint-45 < 100
item[4] 0 ≦ randomPoint-145 < 100
となります。これを公式のようにすると
配列[x]のエリアに抽選の値があるかどうかの判定は
・x=0の時
抽選の値<配列[x]
・x>0の時
抽選の値-配列[x-1]<配列[x]
この式が成立する配列[x]のアイテムが抽選の結果となりますね。
そしてこの処理を順番にしているのがif文の中の処理になっています。
if (randomPoint < probs[i])
{
return i;
}
else
{
//ランダムポイントが重みより大きいならその値を引いて次の要素へ
randomPoint -= probs[i];
} return probs.Length - 1;最後に、このコードではrandomPointが重みの最大数だった場合に、配列の最後の要素を返すように処理しています。
この抽選では重みの総数にかける乱数が1.0の場合、randomPointが重みの最大数になります。
この場合forループの中で最後までループさせてもrandomPoint < probs[i]が成立する事はなく戻り値を返す事なくforループを抜け出してしまいます。
そうなった時にprobs.Length に 1を引いた値=最後要素の値を返しています。
このコードをUnityのでボタンUIにアタッチさせて押すとGatyaメソッドが実行されるようにすると
コンソールに以下のように表示されました。

今回のガチャでは3が帰ってきたのでitem[3]を引き当てた事になります。
item[3]は重み100なので確率的には高いですね。
今回はコンソールに表示させただけですが、例えばresultが0の時はこのアイテムが出現、
みたいな処理をしてあげれば重み付きの抽選結果をゲームに反映させることが出来そうですね。
この抽選では、各アイテムの出現確率%をコードの中では求めていません。
計算式を入れて%に置き換えて割り出すこともできるかもしれませんが、それはただ0〜100の範囲に重みを拡大縮小しているだけなので意味が無いからです。

当選確率が100%を超えることはないから0〜100%のどこに抽選結果があるか?で説明したふる
まとめ
重み付きの抽選方法は
・抽選対象に重み=当たりやすさを振り分ける
・(抽選対象の重み/重みの総数)で当選確率が決まる
・全ての抽選対象を重みの値分並べて、抽選した値がどのエリアにいるかを不等式で確認する
・当たりやすさで抽選管理しているので、後からの追加が安易

ここまで付き合ってくれて本当にありがとう!
参考
実は、この乱数の扱い方はUnityのドキュメント「重要なクラス – Random」内の確率の異なるアイテムの選択という項目でも言及されています。
この記事のコードに関してはこのドキュメント内のサンプルコードを参考にしています。
※このブログは、UnityTechnologiesまたはその関連会社が後援または提携しているものではありません。「Unity」は、UnityTechnologiesまたはその関連会社の米国およびその他の国における商標または登録商標です。



